알고리즘 ] 트리순회 : 전위순회·중위 순회·후위 순회, 예제문제(백준 2250)

 

정의

---

트리 순회(Tree traversal)는 트리 구조에서 각각의 노드를 정확히 한 번만 체계적인 방법으로 방문하는 과정을 말한다. 

 

특징 / 특이사항

---

트리 순회에는 전위 순회(pre-order), 중위 순회(in-order), 후위 순회(post-order) 등의 방법이 있다. 

재귀로 구현한다. 

 

알고리즘 별 특징

---

1) 전위 순회

트리를 복사하거나 전위 표기법을 구하는데 주로 사용된다. 

트리를 복사할 때는 트리를 생성할 때 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문이다. 

출처 : https://yoongrammer.tistory.com/70

순회 결과 : A→B→D→E→C→F→G

 

2) 중위 순회

출처 : https://yoongrammer.tistory.com/70

 

순회 결과 : D→B→E→A→F→C→G

 

2) 후위 순회

후위 순위는 트리를 삭제하는 데 사용된다.

부모 노드를 삭제하기 전에 자식 노드를 삭제하는 순으로 삭제해야 하기 때문이다.

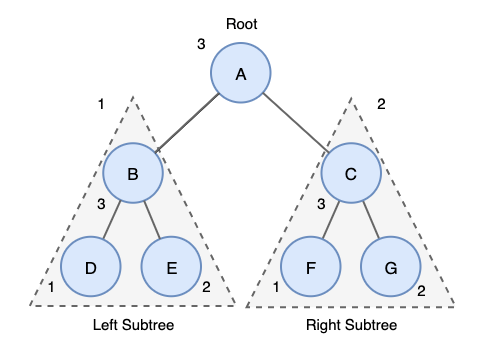
출처 : https://yoongrammer.tistory.com/70

 

순회 결과 : D→E→B→F→G→C→A

---

전위 순회, 중위 순회, 후위 순회 구현

---

위의 tree를 class로 구현하면 아래와 같다.

const tree = {};

class Node {
  constructor(data, left, right) {
    this.data = data;
    this.left = left;
    this.right = right;
  }
}

// 자식이 없을 때는 . 으로 표현
const nodes = ['A B C', 'B D E', 'C F G', 'D . .', 'E . .', 'F . .', 'G . .'];
nodes.forEach((n) => {
  const [node, left, right] = n.split(' ');
  tree[node] = new Node(node, left, right);
});

console.log(tree);

 

전위 순회, 중위 순회, 후위 순회는 위치만 조정하여 재귀로 간단히 구현할 수 있다.

// 전위순회
function pre_order(node) {
  console.log(node.data);

  if (node.left !== '.') {
    pre_order(tree[node.left]);
  }

  if (node.right !== '.') {
    pre_order(tree[node.right]);
  }
}

// 중위순회
function in_order(node) {
  if (node.left !== '.') {
    in_order(tree[node.left]);
  }

  console.log(node.data);

  if (node.right !== '.') {
    in_order(tree[node.right]);
  }
}

// 후위순회
function post_order(node) {
  if (node.left !== '.') {
    post_order(tree[node.left]);
  }

  if (node.right !== '.') {
    post_order(tree[node.right]);
  }

  console.log(node.data);
}

위의 그래프를 각각의 순회로 실행하면 

pre_order(tree['A']);
console.log('_______________________________');
in_order(tree['A']);
console.log('_______________________________');
post_order(tree['A']);

다음과 같은 결과를 얻을 수 있다.

A B D E C F G
_______________________________
D B E A F C G
_______________________________
D E B F G C A

 

---

예제문제

---

1. 백준 2250번 : 트리의 높이와 너비

https://www.acmicpc.net/problem/2250

2250번: 트리의 높이와 너비

해당 문제를 풀이하려면 아래의 내용을 구현해야 한다.

1. 입력받은 정보를 트리로 구현한다.
2. 트리의 루트 노드를 찾는다.
3. 한열에는 한 노드만 존재하는데,
   열 번호가 중위 순회 결과와 같으므로 중위 순회를 이용하여 노드의 열 번호 체크
4. 각 노드의 레벨 체크
5. 같은 레벨일 때 노드의 열 번호가 가장 작은 것과 가장 큰 것 찾기
6. 열 번호의 차이가 가장 넓은 곳 찾기

[ 예제의 데이터 ]

19
1 2 3
2 4 5
3 6 7
4 8 -1
5 9 10
6 11 12
7 13 -1
8 -1 -1
9 14 15
10 -1 -1
11 16 -1
12 -1 -1
13 17 -1
14 -1 -1
15 18 -1
16 -1 -1
17 -1 19
18 -1 -1
19 -1 -1

위의 데이터를 그래프로 나타내면 다음과 같다. 

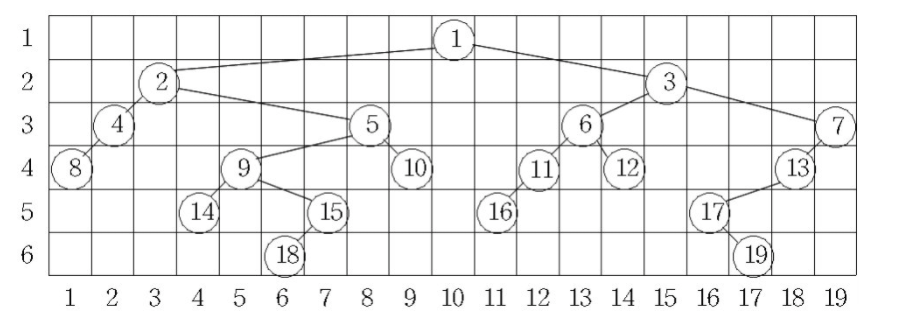
이 그래프를 중위 순회했을 때 순회 결과를 숫자로 나타내면 아래의 열 번호와 같은 것을 알 수 있다.

우선 위의 6가지를 구현하기 위해 필요한 변수들을 선언한다. 

// 트리
const tree = {};

// 같은 레벨 중 가장 작은 열을 check 
const levelMin = [];

// 같은 레벨 중 가장 큰 열을 check
const levelMax = [];

// 루트노드
let root = -1;

// 순회번호
let x = 1;

// 레벨 check
let levelDepth = 1;


// 노드
class Node {
	constructor(data, left, right) {
		this.parent = -1;
		this.data = data;
		this.left = left;
		this.right = right;
	}
}

 

그리고 트리에 정보를 넣기 전 변수를 초기화해준다. 

	// 들어올 데이터가 몇번 노드까지 있는지 확인한다.
    const N = Number(testCase);
    
	levelMin.push(N);
	levelMax.push(0);

	[...Array(N).keys()].forEach((n) => {
		tree[n + 1] = new Node(n + 1, -1, -1);
		levelMin.push(N);
		levelMax.push(0);
	});
    
    
    // tree에 1번부터 N번까지 노드를 초기화 해준다.
    // level min, max 를 각각 초기화 해준다.
    // levelMin = [ N, N, N, N, N, N, N, N  ...]
    // levelMax = [ 0, 0, 0, 0, 0, 0, 0, 0  ...]

level min과 max는 각각의 index가 level로 사용될 예정이다. 

자, 그럼 이제 위의 6가지를 구현해 보자. 

 

1) 입력받은 정보를 트리로 구현한다.

	// 부모, 자신, 왼쪽, 오른쪽 자식 넣기
	nodes.forEach((n) => {
		const [node, left, right] = n.split(' ').map((e) => Number(e));
		tree[node].left = left;
		tree[node].right = right;

		if (left !== -1) {
			tree[left].parent = node;
		}
		if (right !== -1) {
			tree[right].parent = node;
		}
	});

 

2) 트리의 루트 노드를 찾는다.

	// 데이터를 다 넣은 후, parent 값이 없는 노드를 찾는다.
    
    [...Array(N).keys()].forEach((n) => {
		if (tree[n + 1].parent === -1) {
			root = n + 1;
		}
	});

 

3) 한열에는 한 노드만 존재하는데, 열 번호가 중위 순회 결과와 같으므로 중위 순회를 이용하여 노드의 열 번호 체크
4) 각 노드의 레벨 체크
5) 같은 레벨일 때 노드의 열 번호가 가장 작은 것과 가장 큰 것 찾기

// 중위 순회를 돌며 3가지를 구현해보자.

function inOrder(node, level) {
	// 레벨 체크
	levelDepth = Math.max(levelDepth, level);

	if (node.left !== -1) {
		inOrder(tree[node.left], level + 1);
	}

	// 같은 레벨에서 가장 큰열, 가장 작은 열을 찾는다.
	levelMin[level] = Math.min(levelMin[level], x);
	levelMax[level] = Math.max(levelMax[level], x);
    // 순회번호(열번호 체크)
	x += 1;

	if (node.right !== -1) {
		inOrder(tree[node.right], level + 1);
	}
}

위의 코드로 중위 순회를 돌면, 

level을 index 삼아 x(열 번호)를 배열에 넣어줄 수가 있다.

첫 번째 순회하게 되는 8번 노드는 x(열 번호) = 1을 가지게 된다. 

이때, 재귀를 통해 level은 4가 되므로 min과 max 배열의 4번째 값은 각각 1이 된다. 

순회 순서대로 각각의 index에 값을 가지게 되다가

8번 노드와 같은 레벨을 가진 9번 노드를 만나게 된다. 

이때, 9번 노드의 x(열 번호) = 5 이므로 1 값을 가지고 있는 min 배열에서는 변화가 없고, 1값을 가지고 있는 max 배열은 5로 값을 바꾸게 된다. 

노드 9까지 왔을 때 중위 순위 결과를 log로 찍어보면 다음과 같다.

lev min : 1 [ 19, 19, 19, 19, 1, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19 ]
lev max : 1 [ 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

lev min : 2 [ 19, 19, 19, 2, 1, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19 ]
lev max : 2 [ 0, 0, 0, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

lev min : 3 [ 19, 19, 3, 2, 1, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19 ]
lev max : 3 [ 0, 0, 3, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

lev min : 4 [ 19, 19, 3, 2, 1, 4, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19 ]
lev max : 4 [ 0, 0, 3, 2, 1, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

lev min : 5 [ 19, 19, 3, 2, 1, 4, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19 ]
lev max : 5 [ 0, 0, 3, 2, 5, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

 

이렇게 구한 levelMin과 levelMax 배열의 값은 아래와 같다.

lev min: [ 19, 10, 3, 2, 1, 4, 6, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19 ]
lev max: [ 0, 10, 15, 19, 18, 16, 17, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

 

6) 열 번호의 차이가 가장 넓은 곳 찾기

	// 각 인덱스의 차이를 구해 가장 넓은 차이를 가진 곳을 찾는다.
    
    let resultLevel = 1;
	let resultWidth = levelMax[1] - levelMin[1] + 1;

	[...Array(levelDepth + 1).keys()].forEach((n) => {
		if (n > 1) {
			let width = levelMax[n] - levelMin[n] + 1;
			if (resultWidth < width) {
				resultLevel = n;
				resultWidth = width;
			}
		}
	});

 

전체 코드

const readline = require('readline');
const rl = readline.createInterface({
	input: process.stdin,
	output: process.stdout,
});

const tree = {};
const levelMin = [];
const levelMax = [];
let root = -1;
let x = 1;
let levelDepth = 1;

class Node {
	constructor(data, left, right) {
		this.parent = -1;
		this.data = data;
		this.left = left;
		this.right = right;
	}
}

function inOrder(node, level) {
	levelDepth = Math.max(levelDepth, level);

	if (node.left !== -1) {
		inOrder(tree[node.left], level + 1);
	}

	levelMin[level] = Math.min(levelMin[level], x);
	levelMax[level] = Math.max(levelMax[level], x);
	x += 1;

	if (node.right !== -1) {
		inOrder(tree[node.right], level + 1);
	}
}

function solution(arr) {
	const [testCase, ...nodes] = arr;
	const N = Number(testCase);
	levelMin.push(N);
	levelMax.push(0);

	[...Array(N).keys()].forEach((n) => {
		tree[n + 1] = new Node(n + 1, -1, -1);
		levelMin.push(N);
		levelMax.push(0);
	});

	// 데이터 넣기
	nodes.forEach((n) => {
		const [node, left, right] = n.split(' ').map((e) => Number(e));
		tree[node].left = left;
		tree[node].right = right;

		if (left !== -1) {
			tree[left].parent = node;
		}
		if (right !== -1) {
			tree[right].parent = node;
		}
	});

	// 루트찾기
	[...Array(N).keys()].forEach((n) => {
		if (tree[n + 1].parent === -1) {
			root = n + 1;
		}
	});

	// 중위순회
	inOrder(tree[root], 1);

	let resultLevel = 1;
	let resultWidth = levelMax[1] - levelMin[1] + 1;

	[...Array(levelDepth + 1).keys()].forEach((n) => {
		if (n > 1) {
			let width = levelMax[n] - levelMin[n] + 1;
			if (resultWidth < width) {
				resultLevel = n;
				resultWidth = width;
			}
		}
	});

	console.log(`${resultLevel} ${resultWidth}`);
}

const input = [];
rl.on('line', function (line) {
	input.push(line.trimRight());
}).on('close', function () {
	solution(input);
	process.exit();
});